Herhangi bir üçgende, üçgenin bir köşesinden karşı kenara çizilen bir doğru parçasının uzunluğu, üçgenin diğer kenarları ve doğru parçasının karşı kenarda ayırdığı parçalar arasında bir bağıntı vardır. Bu bağıntı esasında, iki farklı üçgende ortak açı kullanılarak, cosinüs teoremi uygulanmasından ibaret olup, verilen üçgenlerden birinden ortak açının cosinüs değeri üçgenin kenarları cinsinden ifade edildikten sonra diğer üçgende ortak açının cosinüs değerine bulunan bu eşitlik yazılır. Daha sonra düzenlemeler yapıldıktan sonra Stewart bağıntısı elde edilir.
Net Fikir » Mayıs 2018 Arşivi
Stewart Teoremi ve ispatı
Bir üçgenin köşelerinden birinden karşı kenara çizilen herhangi bir doğru parçasının uzunluğu, Stewart teoremi ile kolayca bulunabilir. Teoremin güzel tarafı, üçgende herhangi bir açı veya özel durum gerektirmemesidir. Herhangi bir üçgende hiç bir açı değeri verilemden eğer teoremde kullanılan parça uzunlukları biliniyorsa bu bağıntı rahatlıkla kullanılabilir. Üçgende bir köşeden çizdiğimiz doğru parçası eğer yükseklikse, bu durumlarda Pisagor bağıntısını da kullanabiliriz. Ya da çizilen doğru parçası kenarortay veya açıortay ise o zaman bunların ilgili olduğu özellikleri ve teoremleri de kullanabiliriz. Ancak elimizde hiçbir bilgi yoksa o zaman bu teoremi kullanmak daha mantıklı olacaktır.
Koordinatları bilinen üçgen alanı
Köşe koordinatları bilinen üçgenin alanını bulmak için, vektör bileşenlerin determinant kuralından yararlanılır. Determinantta SARRUS Kuralı olarak bilinen determinant hesabı, üçgenlerde köşe koordinatları bilindiği zaman veya köşe koordinatları bir şekilde bulunabildiği zaman, alan hesabında uygulanabilir.
Bunun için üçgenin verilen köşe koordinatları, sırasıyla alt alta yazılır. İlk yazılan koordinat, tekrar en alta ilave edilir. Bu şekilde yazılış tamamlandıktan sonra sağ ve sol tarafa doğru çapraz olarak, her terim birbiriyle çarpılır. SAğ taraftaki çarpım sonucu pozitif, sol taraftaki çarpım sonucu da negatif olarak alınıp bu iki sonuç toplanır. Elde edilen sonuç, üçgen alanı sorulduğu için ikiye bölünerek, üçgenin alan değeri bulunur.
Alan negatif olamayacağından, sonuç negatif çıksa dahi mutlak değer içinde kabul edilerek pozitif alan yazılır. Üç köşesinin koordinatları bilinen bir üçgenin alanı, üçgen analitik düzlemde çizilerek de bulunabilir. Bu durumda, üçgenin yüksekliğini tespit etmek gerekebilir. İki nokta arası uzaklık formülünden de üçgenin taban kenarı uzunluğu bulunur.
Köşe koordinatlarından herhangi ikisinin apsisleri yada ordinatları eşit ise üçgenin kenarlarından biri eksenlere paralel olur. Bu durumda üçgenin alanı, çizilerek yüksekliği kolayca elde edilir ve alanı rahatlıkla hesaplanabilir.
Bir üçgenin alanının sıfır çıkması, köşe koordinatları olarak verilen üç noktanın doğrusal üç nokta olduğunu gösterir. Yani verilen bu noktalar aynı doğru üzerinde olduklarından üçgen belirtmez.
ÖRNEK: Köşe koordinatları A(1,3), B(-2,4), C(3,5) olan ABC üçgeninin alanını bulunuz. (CEVAP: 4)ÖRNEK: Köşe koordinatları A(-1,7), B(4,4), C(2,0) olan ABC üçgeninin alanını bulunuz. (CEVAP: 13)ÖRNEK: Köşe koordinatları A(0,1), B(5,7), C(2,9) olan ABC üçgeninin alanını bulunuz. (CEVAP: 14)ÖRNEK: Köşe koordinatları A(7,-3), B(-2,1), C(-4,-5) olan ABC üçgeninin alanını bulunuz.(CEVAP: 31)ÖRNEK: Köşe koordinatları A(1,-3), B(5,9), C(-4,-8) olan ABC üçgeninin alanını bulunuz.(CEVAP: 20)
Sinüs ve Cosinüs Fonksiyonları
Trigonometrik Fonksiyonlar merkezi orijin ve yarıçapı 1 br olan birim çember üzerinde gösterilerek buradaki geometri ve analitik bilgileri yardımıyla tanımlanır. Birim çember üzerinde alınan herhangi bir noktanın orijinde oluşturduğu merkezil açının, sinüs ve cosinüs gibi trigonometrik değerleri analitik geometri yardımıyla ifade edilir. Birim çember üzerinden rastgele seçilen bir P noktasının apsis değeri o merkezil açıya ait cosinüs değerini verir. Aynı şekilde P noktasının ordinat değeri o merkezil açıya ait sinüs değerini verir. Aşağıdaki şekilden bu tanım görülebilir.
Cosinüs fonksiyonun koordinat düzlemindeki bölgelere göre işaretleri ve verilen noktanın apsis değerleri aşağıda gösterilmiştir. Şekiller incelendiğinde cosinüs değerinin birim çemberin dışına çıkamadığı görülür. Yani hangi açı değeri alınırsa alınsın cosinüs değeri -1 ile 1 arasında (sınırlar dahil) değer alır. Cosinüs fonksiyonun en büyük değeri, açı 0 derece olduğu zaman olur ki değeri cos0=1 olur. Cosinüs fonksiyonun en küçük değeri, açı 180 derece olduğu zaman olur ki değeri cos180=-1 olur. Açı 90 derece olursa cos90=0 ve açı 270 derece olursa cos270=0 olur.
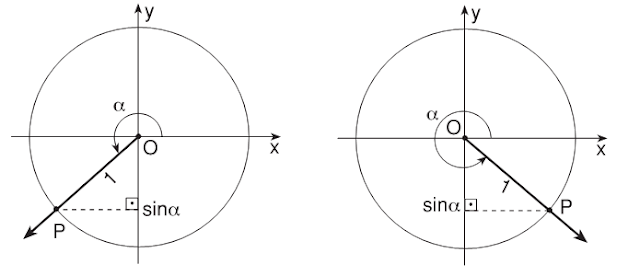
Sinüs fonksiyonun koordinat düzlemindeki bölgelere göre işaretleri ve verilen noktanın ordinat değerleri aşağıda gösterilmiştir. Şekiller incelendiğinde sinüs değerinin birim çemberin dışına çıkamadığı görülür. Yani hangi açı değeri alınırsa alınsın sinüs değeri -1 ile 1 arasında (sınırlar dahil) değer alır. Sinüs fonksiyonun en büyük değeri, açı 90 derece olduğu zaman olur ki değeri sin90=1 olur. Sinüs fonksiyonun en küçük değeri, açı 270 derece olduğu zaman olur ki değeri sin270=-1 olur. Açı 0 derece olursa sin0=0 ve açı 180 derece olursa sin180=0 olur.
Bu bilgilere göre kosinüs ve sinüs fonksiyonlarının tanım ve görüntü kümeleri tanımlanmış olur. Sinüs ve cosinüs fonksiyonlarının görüntü kümesi [-1,1] kapalı aralığıdır.
Birim çember üzerinde bulunan uç noktaların oluşturduğu bazı özel açı değerleri (0,90,180,270 ve 360) için sinüs ve cosinüs değerleri birim çemberdeki apsis ve ordinat değerlerine göre yazılır.
Birim çember üzerinde verilen herhangi bir noktanın oluşturduğu merkezil açının kolları yardımıyla oluşan dik üçgen için, pisagor bağıntısı yazıldığında trigonometrik özdeşlik oluşur.
Verilen bir dik üçgendeki herhangi bir dar açının sinüs ve cosinüs değerleri, dik kenarlar ve hipotenüs uzunluğu yardımıyla tanımlanabilir. Sinüs ve cosinüs fonksiyonlarından yola çıkarak tanjant ve kotanjant fonksiyonları da dik üçgen yardımıyla gösterilir.
Özel bazı dar açılar için dik üçgende sinüs ve cosinüs değerleri, verilen dik kenarlar ve hipotenüs ölçüsüne göre bulunabilir. Bu oranlardan herhangi biri verildiğinde diğer trigonometrik oranlar da dar açıya uygun bir dik üçgen çizilip hesaplanır. Burada açının bulunduğu bölgedeki trigonometrik fonksiyonun işareti önemlidir. Verilen açı öncelikli olarak dar açı karşılığına dönüştürülüp buna bağlı olarak bölgeye göre işareti ile birlikte değeri hesaplanır.
Trigonometrik FonksiyonlarSinüs ve Kosinüs FonksiyonlarıTanjant ve Kotanjant FonksiyonlarıSekant ve Kosekant Fonksiyonları
Aşağıdaki Yazılar İlginizi Çekebilir!!!
En Çok Okunan Yazılar
-
ÖSYM'nin 15/06/2019 Tarihinde gerçekleştirdiği TYT matematik sınavı, farklı tarzda ayırt edici sorular içermekle birlikte, 2018 yılı TY...
-
Bu yazıda Esma-ül Hüsna hakkında kısaca bilgi verildikten sonra Ebced hesabı ile arasındaki ilişkiyi açıklayıp bütün 99 ismin ebced değerle...
-
Dar açıların trigonometrik değerleri hesap makinesi yardımıyla bulunabileceği gibi trigonometrik değerler cetvelinden de bulunabilir. Bunun...
-
Paralelkenar, karşılıklı kenar uzunlukları birbirine eşit olan ve iç açıları toplamı 360 derece olan bir dörtgendir. Paralelkenar, yamuk şe...
-
Herhangi bir dörtgenin alanı köşegen uzunlukları ile köşegenlerin arasında yer alan açının sinüsünün çarpımının yarısı ile hesaplanır. Bura...
-
Çemberde kuvvet alınırken çemberin dışında ve içinde olan noktaya göre kuvvet alma işlemi, noktanın çemberin üzerindeki noktalara uzaklığın...
-
Çocukluğumuzda mutlaka uçurtma yapmayı denemiş veya satın alınan bir uçurtmayı uçurmak için yoğun çaba sarf etmişizdir. Hazır olarak alınanl...
-
Tüm açılarının ölçüsü, 90 derece olan paralelkenara dikdörtgen (mustatil) adı verilir. Paralelkenarın bütün özelliklerini taşır. Karşılıklı ...
-
Köşe koordinatları bilinen üçgenin alanını bulmak için, vektör bileşenlerin determinant kuralından yararlanılır. Determinantta SARRUS Kuralı...
-
LYS Matematik sınavı; son yıllarla kıyaslandığında önceki yılların sorularına benzemekle birlikte biraz daha zorluk derecesi azaltılmış nite...
Matematik Konularından Seçmeler
geometri
(124)
üçgen
(49)
ÖSYM Sınavları
(39)
trigonometri
(35)
çember
(29)
fonksiyon
(28)
sayılar
(25)
alan formülleri
(22)
denklem
(18)
türev
(18)
analitik geometri
(17)
dörtgenler
(17)
limit
(14)
katı cisimler
(10)
koordinat sistemi
(10)
fraktal geometri
(7)
materyal geliştirme
(7)
belirli integral
(6)
asal sayılar
(4)
elips
(3)
tümevarım
(3)
binom açılımı
(2)
hiperbol
(2)










































Lütfen ilgili yazıların altında, yorumlarınızı bizimle paylaşınız. Kırık bağlantıları ve hatalı içerikleri mutlaka bildiriniz. Bizlere güzel dualar ederek destek olunuz.
..KADİR PANCAR...